What Is Associative Property? A Deep Dive Into Its Meaning and Significance
Mathematics is a universal language that governs countless aspects of our daily lives. Among its foundational principles is the associative property, a rule so essential that it influences everything from simple arithmetic to advanced algorithms. This article explores what is associative property, explains its nuances, and highlights its practical importance, ensuring you grasp its essence and relevance. Along the way, we’ll also explore Bulksgo to enhance your learning experience with useful resources.
Understanding What Is Associative Property
It is a mathematical rule stating that when performing addition or multiplication, the way numbers are grouped does not affect the final result. This property simplifies calculations and ensures consistency in problem-solving across different contexts.
For example:
- Addition: (a + b) + c = a + (b + c)
- Multiplication: (a × b) × c = a × (b × c)
This property applies only to addition and multiplication and does not hold true for subtraction or division.
Historical Context of Associative Property
The term “associative” originates from the Latin word “associatus,” meaning “to join together.” Mathematicians as early as the 17th century recognized this principle, although it was formally defined in the 19th century by figures like François-Joseph Servois. Today, it forms the backbone of algebra and other mathematical disciplines.
Logical Basis
Why does the associative property work? It’s rooted in the idea that arithmetic operations like addition and multiplication are commutative and distributive, ensuring flexibility in grouping numbers. This flexibility aids in breaking complex problems into manageable chunks.
Examples in Practice
Addition Example
Let’s say we have three numbers: 2, 3, and 4. Whether we calculate:
- (2 + 3) + 4 = 5 + 4 = 9
or - 2 + (3 + 4) = 2 + 7 = 9,
the result remains consistent.
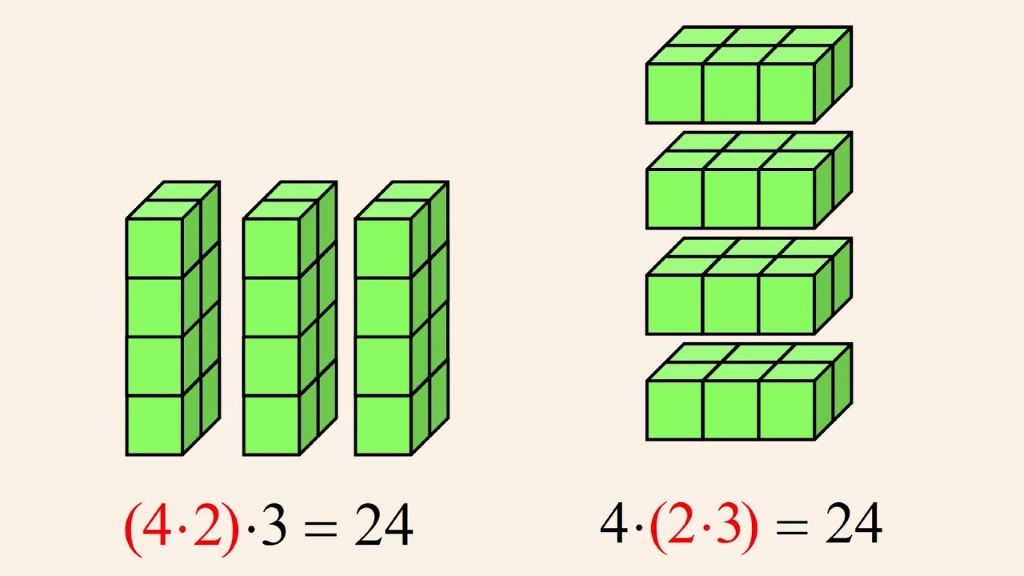
Multiplication Example
Consider the numbers 1, 2, and 3:
- (1 × 2) × 3 = 2 × 3 = 6
or - 1 × (2 × 3) = 1 × 6 = 6.
Contrast with Subtraction and Division
Now, let’s test subtraction:
- (10 − 5) − 2 ≠ 10 − (5 − 2).
Here, the results differ because subtraction is not associative.
Similarly, for division:
- (12 ÷ 4) ÷ 3 ≠ 12 ÷ (4 ÷ 3).
This limitation underscores why the associative property is unique to addition and multiplication.
Practical Applications
Streamlining Mental Math
One of the biggest advantages of the associative property is its role in mental arithmetic. Grouping numbers strategically can make calculations quicker and more efficient.
For instance:
- Instead of calculating (25 + 36) + 14, we can group (36 + 14) first:
25 + (36 + 14) = 25 + 50 = 75.
Computer Algorithms
It is fundamental in computer science, particularly in parallel processing and database operations. Algorithms often rely on this rule to reorder computations for efficiency.
Financial Transactions
In finance, grouping numbers differently during interest calculations or budgeting can simplify large datasets, making the property invaluable in accounting.
The Associative Property in Algebra
Algebra builds upon the associative property, allowing students to manipulate variables confidently. For example:
- (x + y) + z = x + (y + z)
- (a × b) × c = a × (b × c)
This principle ensures the consistency of formulas and equations, providing a solid foundation for higher-level mathematics.
Common Misconceptions
Despite its simplicity, misunderstandings about the associative property persist. Here are some clarifications:
- “All operations are associative.” This is incorrect, as shown with subtraction and division.
- “It changes the order of operations.” Associative property affects grouping, not the sequence.
- “It’s the same as commutative property.” While related, the commutative property deals with order (a + b = b + a), whereas the associative property focuses on grouping.
Importance of Associative Property in Real Life
The associative property is not confined to abstract mathematics; it permeates daily life in surprising ways. When splitting restaurant bills, organizing schedules, or even coding, its principles provide structure and predictability.
For example:
- Splitting $150 among three people can be grouped as ($50 + $50) + $50 or $50 + ($50 + $50), yielding the same result.
If you’re curious about resolving property-related queries, check out How do you make a declaration of no interest in a property for practical insights.
You Might Enjoy: How to Maintain Composite Wood Decks: Easy Tips for Lasting Beauty
Conclusion
The associative property is more than just a mathematical principle; it’s a tool for efficiency, consistency, and logic in problem-solving. By understanding what is it, we not only gain deeper mathematical insights but also enhance our problem-solving skills in practical contexts. Whether simplifying mental math or optimizing algorithms, this property demonstrates the beauty of mathematics in action.
Featured Image Source